As a key component of the power system, power electronic equipment usually exhibits a mixture of continuous and discrete interactions, which has an important impact on the reliability of the power system. The structure of power electronic devices is becoming more and more complex, and the types of faults are also increasing. To ensure the safe, reliable and efficient operation of power electronic devices, it is very important to conduct fault diagnosis research and improve the accuracy of fault diagnosis.
At present, the fault diagnosis methods are mainly divided into data-driven and model-based fault diagnosis methods. The former requires a large amount of historical data as prior knowledge, and the latter needs to establish an accurate physical model of the system. In model-based fault diagnosis, the parameter uncertainty of the system is often not considered, which is easy to cause false alarms. To solve this problem, Armengol J et al. used interval algorithms to study fault detection and diagnosis. Henry and Zolghari proposed a filter method for linear fractional transformation uncertainty models for residual generation and estimation. Ilyas Rahal M et al. established a hybrid fractional graph model of linear fractional transformation for robust fault detection and isolation.
Aiming at the parameter uncertainty of hybrid systems, this paper proposes to use BG-LFT to establish the system parameter uncertainty DHBG model, and generate robust residuals and adaptive thresholds through DHBG to reduce the false positive rate of fault diagnosis. The effectiveness of the proposed method in the robust fault diagnosis of the inverter is verified by simulation.
1 Based on bond graph system uncertainty modeling
1.1 Linear fractional transformation form
Linear Fractional Transformation (LFT) was proposed by Redheffer scholars in 1960 and is widely used in the field of robust control synthesis for multivariate uncertain systems. It has the advantage of decoupling the system into the determined part and the uncertain part. It is a powerful tool to solve the problem of structural singular value, and provides an effective way to construct the parameter uncertainty model of the system. The LFT structure of the model is shown in Figure 1. The determination is indicated by the augmentation matrix M, which represents all the uncertainties (structural, unstructured parameters or modeling uncertainties, measurement noise, etc.). w and z represent the auxiliary input and auxiliary output of the system respectively; u and y represent the real input and the real output of the system, respectively.
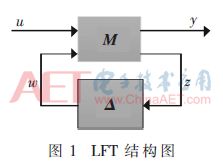
1.2 Bond graph modeling for parameter uncertainty
The key graph theory is used to diagnose the parameter uncertainty robust fault. By establishing the system's diagnostic bond graph model, the Analytical Redundancy Relation (ARR) can be decoupled into the determined part ARRn=f(SSe, SSf). , Se, Sf, MSe, MSf, u, θn) and the indeterminate portion bn = f (SSe, SSF, δ θ θn). Among them, one ARR is represented as a constraint dependent on the system parameter (θ), SSe and SSf are the measurements after the detector is dualized, (Se, Sf, MSe, MSf, u) respectively represent the known input, and θn is the nominal parameter. Δθ is the uncertainty of the parameter. The determined part of the ARR calculates the residual, and the uncertain part calculates the real-time threshold.
The uncertainty of the parameter δθ can be expressed as an additive or multiplicative form, as in equation (1):

Where Δθ and δθ=(Δθ)/θn are respectively expressed as absolute deviations and relative deviations with respect to the nominal value of the parameter θn.
The multiplicative uncertainty of the resistive R component is shown in Figure 2.
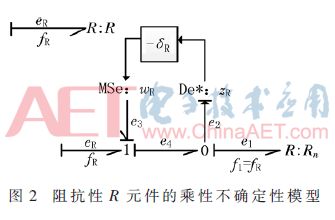
The uncertainty of the impedance type R component is expressed as follows:
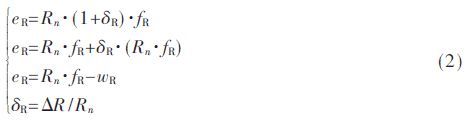
Where Rn, δR, ΔR, eR, and fR represent the nominal value, multiplicative uncertainty, additive uncertainty, potential, and flow of the R element, respectively. wR represents the virtual input of the potential uncertainty after adding the parameter.
The "-" in the bond graph model indicates that the source of the semi-directional arrow points to the corresponding node. The symbols De* and Df* are virtual sensors. The multiplicative uncertainty of other components refers to the resistive R element.
2 Robust analytical redundancy relationship and residual estimation
The robust ARR of the system is obtained by the following three steps:
(1) To avoid the unknown initial conditions of the model, the bond graph model preferentially assigns differential causal relationships.
(2) Based on the coverage causal path, the 0 and 1 nodes contain at least one sensor. The ARR equation can be derived as follows:

3 Parametric troubleshooting example simulation
3.1 Diagnostic Bond Graph Model
The single-phase full-bridge inverter has two bridge arms, which can be seen as a combination of two half-bridge circuits. V1 and V4 are used as a pair, V2 and V3 are used as a pair, and two pairs of IGBTs are turned on at the same time, and two pairs of IGBTs are alternately turned on by 180°, and the structure is as shown in FIG.
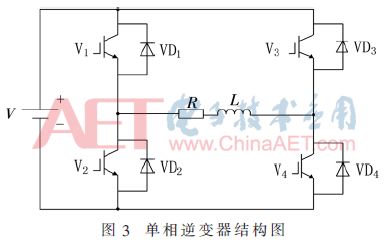
For fault diagnosis of single-phase full-bridge inverters, it is necessary to establish a corresponding diagnostic bond graph model. Therefore, the voltage (current) in the bond graph model is taken as input by introducing a virtual potential (flow) sensor, and the sensor needs to be dualized as much as possible in the diagnostic model. Some sensors do not generate analytical redundancy and do not need to be dualized. According to the above analysis, the causal relationship is re-allocated for the system, and the fault diagnosis bonding graph model of the single-phase full-bridge inverter is established, as shown in Fig. 4.
3.2 Robust analytical redundancy relationship
According to the diagnostic bond graph model shown in Figure 4, two separate parts of the robust ARR are obtained:


Where Se is the known input, SSei and SSfi are the measurements after the detector is dualized, w1/Roni, w1/Roffi and wRoffi are the virtual inputs corresponding to the parameters of each component, δRoffi, δ1/Roffi and δ1/Roni are each Multiplicative uncertainty of component parameters.
3.3 Simulation Results
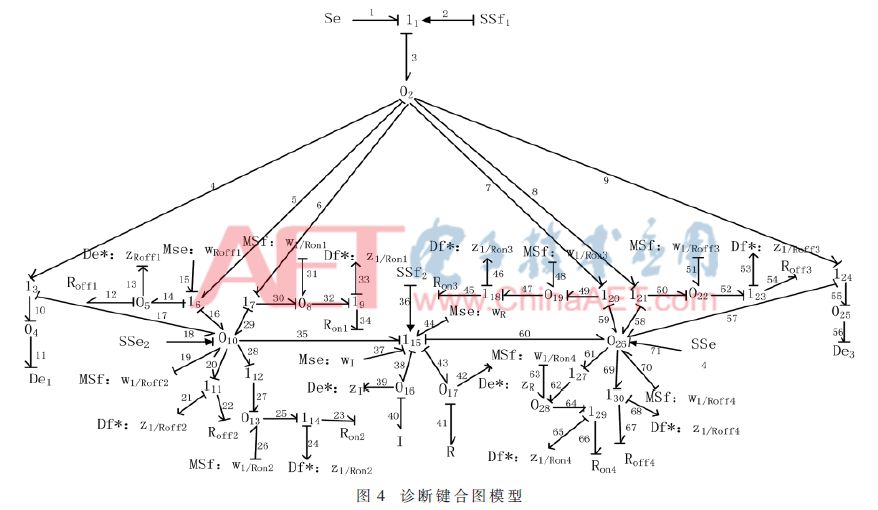
When the system is fault free, the value of the residual is approximately equal to zero or in a small fluctuation state but does not exceed the upper and lower limits of the threshold. If the fault-sensitive residual in the system deviates significantly from zero or even exceeds the threshold, it is considered that a fault has occurred in the system and is reported. If the residual is in the range of (-δθ, δθ), the influence of the component parameter uncertainty on the system or the residual should not cause an alarm. At this time, the system or component is not considered to have failed.
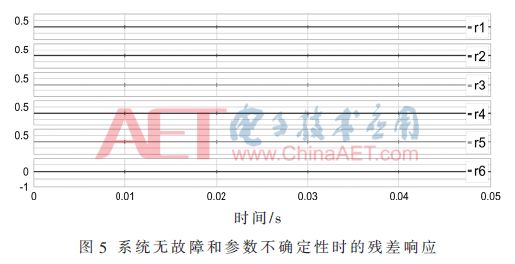
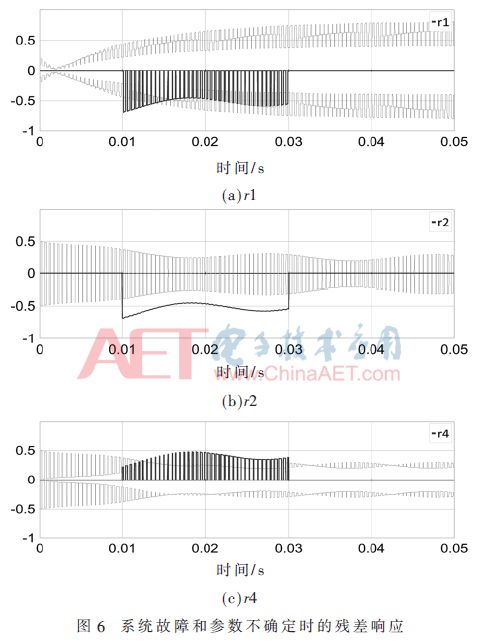
In the simulation, the parameter uncertainty coefficient δθ is 0.05. The simulation results are shown in Figures 5 and 6. Figure 5 shows that the residual is all zero when the system is fault free and all parameters are uncertain. If the residual exceeds the threshold, the system fails. Introducing the parameter Ron1 parameter fault, analyzing and analyzing the redundancy relationship, we can see that the residuals r1, r2 and r4 are sensitive to this fault. As can be seen from Fig. 6, the residuals r1, r2 and r4 obviously exceed the adaptive threshold range, triggering the fault alarm. The Ron1 fault is effectively detected.
4 Conclusion
In this paper, the parameter uncertainty is uncertain in the hybrid system. The traditional fault diagnosis method can not reduce the false alarm. The BG-LFT is used to establish the system parameter uncertain DHBG model, and the adaptive threshold is used to evaluate the residual to make the system robust. The diagnosis can accurately detect the system failure, effectively reduce the false alarm rate, and is verified in the single-phase full-bridge inverter. The experimental results show that the method is effective.
1. Decomposition: biodegradable excess body fat, flat meat, all kinds of stone decomposition, promote the decomposition of food digestion and absorption.
2. Blood purification: Arrange internal environment, purify the blood and improve physical fitness - decomposition, eliminate waste, the blood becomes acid.
3. activation: the pituitary gland to stimulate cell regeneration, a recession is not easy to remember, can not afford to skin wrinkles, youthful beauty delay human aging.
4. Anti-inflammatory antibacterial effect: enzymes can strengthen the fight against white blood cells and remove invading bacteria and purulent matter, the cells speed recovery and enhance wound healing
5. hangover, hangover prevention.
6. For picky eaters, do not like to eat fruits and vegetables children the best nutritional supplements and energy sources.
It contains nutrients more easily absorbed by the body, containing amino acids, polysaccharides, protein components, vitamins B, C, E, and trace elements needed by the body. Long-term use, long-term preservation.
Enzyme Essence Liquid,Liquid Promote Digestion And Absorption,Orange Enzyme Liquid For Health
Guangdong ganzhou , https://www.cn-gangdao.com
