1. Turing machine
According to the current state of the finite state controller and the signed symbols read by each read / write head, one calculation step of the Turing machine can realize one or all of the following three operations.
Change the state in the finite state controller.
Clear the original symbol in the grid under the current read-write head and write a new one.
Independently move any or all read / write heads by one square (L) to the left or one square (R) to the right or stop at the current unit (S).
The k-band Turing machine can be formally described as a 7-tuple (Q, T, I, δ, b, q0, qf), where:
Q is a set of finite states.
T is a finite set of symbols.
I is a collection of input symbols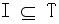 
.
b is the only blank character, b ∈ TI.
q0 is the initial state.
qf is the terminated (or accepted) state.
δ is a movement function.
It is a function that maps from a certain subset of Q × Tk to Q × (T × {L, R, S}) k.
The time complexity T (n) of the Turing machine M is the maximum number of calculation steps it needs to process all inputs of length n. If the Turing machine does not stop for an input of length n, T (n) has no definition for this value of n.
The spatial complexity S (n) of the Turing machine is the sum of the number of squares used in k bands when it processes all inputs of length n. If a read / write head moves to the right indefinitely without stopping, S (n) is also undefined.
Definite Turing Machine
Finite state set Q, state q0: initial state; qy: accepted state; state qn: not accepted state.
Character set {0, 1, b}; where b is a space character.
Conversion function:
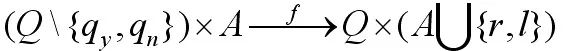
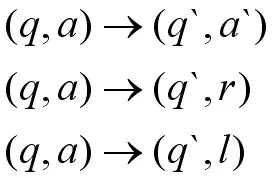
Enter x = 101000b
Execution order:
q0 input 1 (q0, r) moves the head to 0 right
q0 input 0 (q0, r) moves the head to 1 right
q0 input 0 (q0, r) moves the head to 0 right
...
q0 input b (q1, l) Move the head to 0 left
q1 input 0 (q2, b)
q2 Input b (q2, l) Move the head left to 0
q2 input 0 (q3, b)
q3 Enter b (qy, l) to exit
2. P and NP problems
Generally speaking, the problem that can be solved by polynomial time algorithm is regarded as an easy-to-handle problem, and the problem that requires super polynomial time to be solved is regarded as an intractable problem.
There are many problems. On the surface, it does not seem to be more difficult than sorting or graph search. However, so far, people have not found polynomial time algorithms to solve these problems, and no one can prove that these problems require a super polynomial time lower bound.
Under the Turing machine computing model, the computational complexity of this type of problem is still unknown.
In order to study the computational complexity of this kind of problem, people have proposed another more powerful computing model, namely the non-deterministic Turing machine computing model, abbreviated as NDTM (Nondeterministic Turing Machine).
Under the non-deterministic Turing machine calculation model, many problems can be solved in polynomial time.
Non-deterministic Turing machine
In the Turing machine calculation model, the movement function δ is single-valued, that is, for each value in Q´Tk, when it belongs to the domain of δ, Q´ (T´ {L, R, S}) k Only a unique value corresponds to it. This Turing machine is called a deterministic Turing machine, which is abbreviated as DTM (Deterministic Turing Machine).
Non-deterministic Turing machine (NDTM): A k-band non-deterministic Turing machine M is a 7-tuple: (Q, T, I, δ, b, q0, qf). Unlike the deterministic Turing machine, the non-deterministic Turing machine allows the movement function δ to be uncertain, that is, for each value in Q × Tk (q; x1, x2,…, xk), when it belongs to the domain of δ When Q × (T × {L, R, S}) k has a unique subset δ (q; x1, x2, ..., xk) corresponding to it. You can arbitrarily choose a value as its function value in δ (q; x1, x2, ..., xk).
P and NP language definition
P = {L | L is a language that can be accepted by a DTM in polynomial time}
NP = {L | L is a language that can be accepted by an NDTM in polynomial time}
Since a deterministic Turing machine can be regarded as a special case of non-deterministic Turing machines, languages ​​that can be accepted by deterministic Turing machines in polynomial time can also be accepted by non-deterministic Turing machines in polynomial time. So P à NP.
Examples of NP-like languages-clique problem of undirected graphs
The input to this problem is an undirected graph with n vertices G = (V, E) and an integer k. It is required to determine whether the graph G contains a complete subgraph (cluster) of k vertices, that is, to determine whether there is V '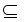 
V, | V '| = k, and for all u, v ∈ V', there is (u, v) ∈ E.
If the graph G is represented by an adjacency matrix and the integer k is represented by a binary string, then an example of the clique problem can be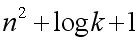 
The binary string representation. Therefore, the group problem can be expressed as language:
CLIQUE = {w # v | w, v∈ {0,1} *, the graph G with w as the adjacency matrix has a cluster of k vertices, where v is the binary representation of k. }
Accept the language's CLIQUE's non-deterministic algorithm: use a non-deterministic selection instruction to select a candidate vertex subset V containing k vertices, and then deterministically check whether this subset is a solution to the clique problem. The algorithm is divided into 3 stages
The first stage of the algorithm decomposes the input string w # v and calculates n =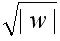 
, And the integer k represented by v. If the input does not have the form w # v or | w | is not a square number, the input is rejected. Obviously, the first stage can be 
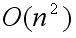Completed within time.
In the second stage of the algorithm, a k-ary subset V of V is selected non-deterministically 
V.
The third stage of the algorithm is to deterministically check the cluster properties of V '. If V 'is a regiment, the input is accepted, otherwise the input is rejected. This can obviously be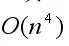 
Completed within time. Therefore, the time complexity of the entire algorithm is 
.
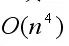The non-deterministic algorithm accepts the language CLIQUE in polynomial time, so CLIQUE∈NP.
NP complete problem
P 
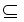NP.
Intuitively, the P-type problem is the easy-to-solve problem class under the deterministic calculation model, and the NP-type problem is the easy-to-verify problem class under the non-deterministic calculation model.
Most computer scientists believe that the NP category contains languages ​​that do not belong to the P category, that is, P ≠NP.
The NP complete problem has a surprising property, that is, if an NP complete problem can be solved in polynomial time, then each problem in NP can be solved in polynomial time, that is, P = NP.
There is currently no NP-complete problem with a polynomial time algorithm.
Third, the approximate algorithm of NP complete problem
So far, all NP-complete problems have no polynomial time algorithm.
For this type of problem, the following strategies can usually be adopted.
Solve only specific examples of problems
Solution with dynamic programming method or branch and bound method
Solve with a probabilistic algorithm
Seek only approximate solutions
Solve with heuristic method
Approximate algorithm performance
If the optimal value of an optimization problem is c *, and the corresponding objective function value of the approximate optimal solution obtained by an approximate algorithm for solving the problem is c, then the performance ratio of the approximate algorithm is defined as
.
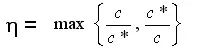
Under normal circumstances, the performance ratio is a function Ï (n) of the problem input scale n, namely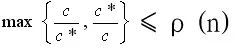 
The relative error of this approximation algorithm is defined as: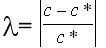 
. If the input scale of the problem is n, there is a function ε (n) such that 
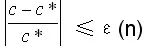Then ε (n) is called the relative error bound of the approximation algorithm. The performance ratio of the approximate algorithm Ï (n) and the relative error bound ε (n) obviously have the following relationship: 
.
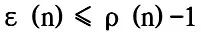Approximate algorithm for traveling salesman problem
Problem description: Given a completely undirected graph G = (V, E), each side (u, v) ∈ E has a non-negative integer cost c (u, v). To find the minimum cost Hamiltonian loop of G.
Some special properties of the travel salesman problem:
For example, the cost function c often has the property of triangular inequality, that is, for any three vertices u, v, w ∈ V, there are: c (u, w) ≤ c (u, v) + c (v, w). When the vertex in graph G is a point on the plane, and the cost between any two vertices is the Euclidean distance between these two points, the cost function c has the property of triangular inequality.
1 Travel salesman problem that satisfies the triangle inequality
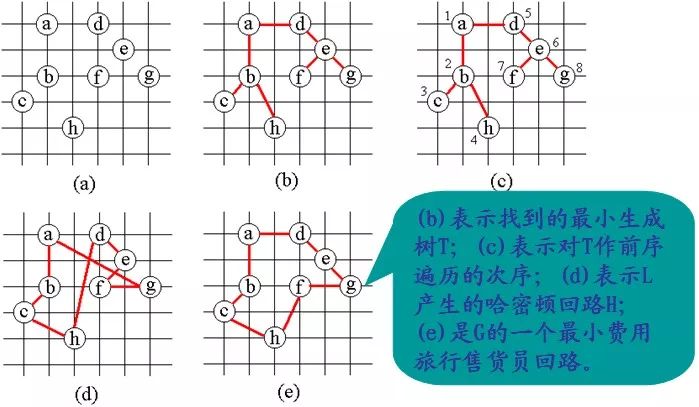
For a given undirected graph G, you can use the algorithm to find the minimum spanning tree of graph G to design an algorithm that finds an approximately optimal travel salesperson loop.
void approxTSP (Graph g)
{
Choose any vertex r of g;
Use the Prim algorithm to find a minimum spanning tree T with weighted graph g rooted at r;
The vertex table L obtained by traversing the tree T in the previous order;
Add r to the end of table L, form a loop H in the order of vertices in table L, and return as the calculation result;
}
When the cost function satisfies the triangle inequality, the cost of the travel salesperson loop found by the algorithm will not exceed twice the cost of the optimal travel salesperson loop.
achieve
/ * Topic: Approximation Algorithm-Travel Salesman Problem
* Author: chinazhangjie
* Email:
* Development language: C ++++
* Development environment: Virtual Studio2005
* Time: 2010.12.06
* /
#include
#include
#include
using namespace std;
structTreeNode
{
public:
TreeNode (intnVertexIndexA = 0, intVerVerIndexIndex = 0, intWeight = 0)
: m_nVertexIndexA (nVertexIndexA),
m_nVertexIndexB (nVertexIndexB),
m_nWeight (nWeight)
{}
public:
intm_nVertexIndexA;
intm_nVertexIndexB;
intm_nWeight;
};
classMST_Prim
{
public:
MST_Prim ()
{}
MST_Prim (const vector> & vnGraph)
{
m_nvGraph = vnGraph;
m_nNodeCount = (int) m_nvGraph.size ();
}
void SetData (const vector> & vnGraph)
{
m_nvGraph = vnGraph;
m_nNodeCount = (int) m_nvGraph.size ();
}
//
const vector & GetMSTree () const
{
returnm_tnMSTree;
}
//
const vector> & GetGraph () const
{
return m_nvGraph;
}
void DoPrim ()
{
// Whether to be visited flag
vector bFlag (m_nNodeCount, false);
bFlag [0] = true;
intnMaxIndexA;
intnMaxIndexB;
intj = 0;
while (j
intnMaxWeight = numeric_limits :: max ();
// Find the current shortest path
inti = 0;
while (i
if (! bFlag [i]) {
++ i;
continue;
}
for (intj = 0; j
if (! bFlag [j] && nMaxWeight> m_nvGraph [i] [j]) {
nMaxWeight = m_nvGraph [i] [j];
nMaxIndexA = i;
nMaxIndexB = j;
}
}
++ i;
}
bFlag [nMaxIndexB] = true;
m_tnMSTree.push_back (TreeNode (nMaxIndexA, nMaxIndexB, nMaxWeight));
++ j;
}
// output result
/ * for (vector :: const_iterator ite = m_tnMSTree.begin ();
ite! = m_tnMSTree.end ();
++ ite) {
cout "
} * /
}
private:
vector> m_nvGraph; // undirected connected graph
vector m_tnMSTree; // minimum spanning tree
int m_nNodeCount;
};
classAA_TSP
{
public:
AA_TSP (const vector> & vnGraph)
{
m_mstPrim.SetData (vnGraph);
}
void Get_AA_Path ()
{
m_mstPrim.DoPrim ();
vector mstree = m_mstPrim.GetMSTree ();
vector> graph = m_mstPrim.GetGraph ();
intiweight = 0;
for (vector :: const_iterator ite = mstree.begin ();
ite! = mstree.end ();
++ ite) {
cout "
iweight + = (* ite) .m_nWeight;
}
cout "
iweight + = graph [mstree [0] .m_nVertexIndexA] [mstree [mstree.size ()-1] .m_nVertexIndexB];
cout
}
private:
MST_Prim m_mstPrim;
};
intmain ()
{
const intcnNodeCount = 5;
vector> graph (cnNodeCount);
for (size_ti = 0; i
graph [i] .resize (cnNodeCount, numeric_limits :: max ());
}
graph [0] [1] = 5;
graph [0] [2] = 1;
graph [0] [3] = 2;
graph [0] [4] = 3;
graph [1] [0] = 5;
graph [1] [2] = 4;
graph [1] [3] = 2;
graph [1] [4] = 2;
graph [2] [1] = 4;
graph [2] [0] = 1;
graph [2] [3] = 5;
graph [2] [4] = 3;
graph [3] [1] = 2;
graph [3] [2] = 5;
graph [3] [0] = 2;
graph [3] [4] = 2;
graph [4] [1] = 2;
graph [4] [2] = 3;
graph [4] [3] = 2;
graph [4] [0] = 3;
AA_TSP aa (graph);
aa.Get_AA_Path ();
return0;
}
2 General travel salesman issues
In the general case where the cost function does not necessarily satisfy the triangle inequality, there is no polynomial time approximation algorithm with a constant performance ratio to solve the TSP problem, unless P = NP. In other words, if P ≠NP, for any constant Ï> 1, there is no polynomial time approximation algorithm for the travel salesman problem with a performance ratio Ï.
Furniture Sofa And Mattress Staple
Zhejiang Best Nail Industrial Co., Ltd. , https://www.beststaple.com