Noise and power consumption of IoT smart sensors

For those who develop smart sensors for IoT applications, the relationship between performance and power consumption is the most subtle trade-off. In a wide performance space, noise is often an important factor to evaluate because it limits the choice of devices for critical functional blocks in smart sensors, thereby increasing the power consumption burden. In addition, the noise characteristics largely determine the filtering requirements, which in turn affects the sensor's ability to respond to rapid changes in conditions and prolong the time required to produce high quality measurements.

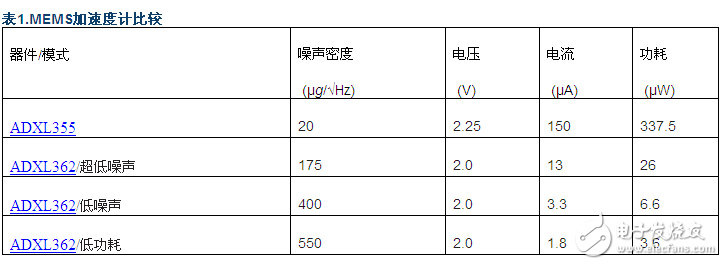
In applications that support continuous observation (sampling, processing, communication), system architects often have to resolve the opposite relationship between noise and power consumption, because the lowest noise solution is rarely the right and the lowest power solution (specifically For the functional category of the device). For example, MEMS accelerometers are often used as the core sensor for remote tilt measurement systems. Table 1 shows the key features of two different products that provide current industry-leading noise or power performance: ADXL355 (low noise) and ADXL362 (low power).

Table 1 consists of four rows, three of which correspond to the optional mode of operation of the ADXL362, and the remaining row gives the main indicators of the ADXL355. Starting from the critical boundary of this trade-off space, the ADXL355's noise is almost 27 times lower than the lowest power mode ADXL362, but the former consumes much more power. Performance requirements for more challenging applications may need to consider the highest performance mode of the ADXL362, where the ADXL355 is 9 times less noisy, but the ADXL362 consumes 13 times less power.

In applications that do not require continuous observation, the relationship between average power consumption and noise becomes more meaningful. Perhaps unbelievable, but the relationship between noise and power consumption may even become complementary. This is definitely good news for developers. Because in previous designs, developers might have missed the opportunity because it was difficult to determine whether power consumption or performance dominated their design. Now, without waiting for others to make a decision in this trade-off, smart sensor architects can quantify the relevant options within the trade-offs; this will redefine the architect's work.

In order to quantify the relevant options for a particular application, you first need to make some assumptions about the signal chain, so you can start with a conceptual architecture. Figure 1 is a general example of a smart sensor architecture that includes the most common features.

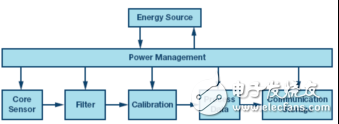
Figure 1. Smart Sensor Architecture

The signal chain in the smart sensor node begins with the core sensor function. The most basic form of core sensor, also known as a transducer, converts physical conditions or attributes into representative electrical signals. The scale factor of a sensor describes the linear relationship of its electrical response to the physical properties or conditions it monitors. For example, a temperature sensor that provides an analog output (such as the AD590) has a scale factor unit of mV/°C; a digital accelerometer (such as the ADXL355) has a scale factor expressed in LSB/g or code/g.

The next functional block of the signal chain (Figure 1) is the filter. The role of this level is to reduce the noise in the frequency bands that the core sensor may support, but not the application. In vibration monitoring applications, this may be a bandpass filter that separates random vibrations from specific spectral features that may indicate machine life degradation. In the tilt sensor, this may be a simple low pass filter, such as a moving average filter. In this case, the duration is an important trade-off between setup time and filter output residual noise. Figure 2 shows an example of the ADXL355 Allen variance curve, which shows the uncertainty (noise) of the measurement relative to the mean time at which the measurement was produced.

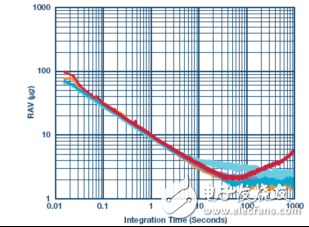
Figure 2. Allen's variance curve: ADXL355 and ADXL362

The function of the calibration function is to improve the measurement accuracy by applying a correction formula. In extremely demanding applications, measurements are typically made under strictly controlled conditions, and such correction formulas are obtained by directly observing the sensor response. For example, in tilt sensor applications, the calibration process involves observing the output of the MEMS accelerometer in a number of different directions relative to gravity. The general goal of this observation is to observe the response of the sensor to a sufficient number of orientations to solve all 12 correction factors (m11, m12, m13, m21, m22, m23, m31, m32, m33) in the following relationship (see Equation 1). , bx, by, bz):

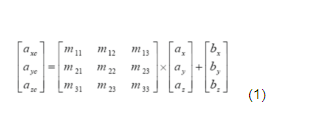
The correction factors in Equation 1 are used to handle bias, sensitivity, and alignment errors. This formula can also be extended to include higher order sensor characteristics (non-linearity) or environmental correlation (temperature, power level).

Mario Kit

Guangzhou Ruihong Electronic Technology CO.,Ltd , https://www.callegame.com